Question

You want to know if high-school females score differently than high-school males on a standardized test. You take a random sample of 28 males and 27 females from high schools across the country and record their scores. Which confidence interval would you use to analyze these data?

Answer 1

`\bar{x_(1)} - \bar{x_(2)} \pm t*\sqrt{s((1)/(n_(1)) + (1)/(n_(2)))}`

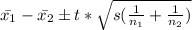
Explanation:

Random sample size of males, n₁ = 28

Random sample size of males, n₂ = 27

Here,

If n₁ < 30 & n₂ < 30,

we use t-distribution

Therefore,

The confidence interval chosen will be

⇒
`\bar{x_(1)} - \bar{x_(2)} \pm t*\sqrt{s((1)/(n_(1)) + (1)/(n_(2)))}`

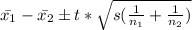
Here,

`\bar{x_(1)}` is mean of sample n₁

and,

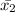`\bar{x_(2)}` is mean of sample n₂

s is the standard deviation

the value of 't' can be obtained from the standard t- distribution table