Answer:
The answer is 80,1 °C
Step-by-step explanation:
Let´s start from the mass of the sample and the heat capacities:
First of all, we must calculate an average heat capacity. That's because we have a mixture and it is unknown the heat capacity of the whole sample.
The way we should do this calculation is as follows:
(1)
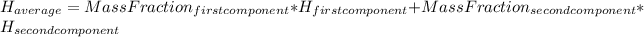
For example, the mass fraction of Fe is simply:
(2)

If you combine the equations (1) and (2) you have:
(3)
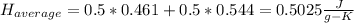
Once calculated the average heat capacity we can solve the problem taking into account the corresponding equation:
(4)
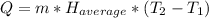
Remember that:
Q: Heat gained or lost
m: Mass of the sample you want to analize
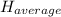 : The value obtained in equation (3)
: The value obtained in equation (3)
 : Final temperature of the sample
: Final temperature of the sample
 : Initial temperature of the sample
: Initial temperature of the sample
Now we must replace the problem data in equation (4)
Take into account:
- Heat gained in a system have a positive value
- Heat lost in a system have a negative value
- In this problem the sample loses 200 J, for this reason
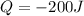
- The mass of the whole sample is: 10g of Fe + 10g of Ti = 20g of sample
- The temperatures must be in absolute units of temperature (these are: rankine or kelvin)
- The initial temperature of the system is 100°C or 373K
Now we are ready to use equation (4):
(5)
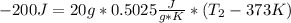
It is clear that the unknown in equation (5) is

The next step is to calculate
 . Don't forget the signs; these are important.
. Don't forget the signs; these are important.
Key concept: Since the system is loosing heat, the final temperature of the system (
 ) should be lower than the initial temperature (
) should be lower than the initial temperature (
 )
)