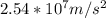Question

According to the Guinness Book of World Records (1990 edition, p. 169), the highest rotary speed ever attained was 2010 m/s (4500 mph). The rotating rod was 15.9 cm (6.3 in) long. Assume the speed quoted is that of the end of the rod. What is the centripetal acceleration of the end of the rod? Answer in units of m/s 2 .

Answer 1

When a body performs a uniform circular motion, the direction of the velocity vector changes at every moment. This variation is experienced by the linear vector, due to a force called centripetal, directed towards the center of the circle that gives rise to centripetal acceleration, the mathematical expression is given as,

`a = (v^2)/(r)`

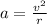
Where,

v = Tangential Velocity

r = Radius

The linear velocity was 2010m/s in a radius of 0.159m, then the centripetal acceleration is

`a = (2010^2)/(0.159)`

`a = 2.54*10^7m/s^2`

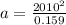
Therefore the centripetal acceleration of the end of the rod is
`2.54*10^7m/s^2`