Question

Set up and solve a quadratic equation: The screen of a new laptop has a diagonal of 17 inches. If the length of the computer is 1 inch less than twice the width, find the dimensions of the computer.

Answer 1

width = 8 in

height = 15 in

Explanation:

considering the pythagorous theorem

`hypotenuse^(2) = height^(2) +base^(2)\\`

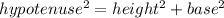
hypotenuse = length of diagonal = 17 in

base = width = w

height = L = 2w -1

`(17)^(2)=(2w-1)^(2)+w^(2)\\289 = 4w^(2)-4w+1+w^(2)\\288=5w^(2)-4w\\5w^(2)-4w-288=0`

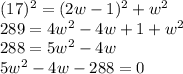
applying the quadratic formula two roots for w:

`w=\frac{-b \pm \sqrt{b^(2)-4ac} }{2a}\\b = -4\\a= 5\\c= -288\\w=\frac{-(-4) \pm \sqrt{(-4)^(2)-4(5)(-288)} }{2(5)}`

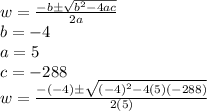
w = 8 ; w = -7.2

as width cannot be negative

so

w = 8 in

L = 2w -1

L = 16 -1

L = 15 in