Question

A string of length 1.3 m is oscillating in a standing wave pattern. If the tension in the string is 430 N, the string has a mass of 23 g/m, and the amplitude of the oscillations is 2.1 mm, what is the maximum speed of a point on the string when it is oscillating in the fundamental mode?

A

1.4 m/s

B

0.69 m/s

C

0.45 m/s

D

0.22 m/s

E

2.8 m/s

Answer 1

To solve this problem we will use the concepts related to the speed of a string which is given by the applied voltage and the linear mass density of it. With the speed value we can find the fundamental frequency that will serve as a step to find the maximum speed through the relation of Amplitude and Angular Speed. So:

`v = \sqrt{(T)/(\mu_e)}`

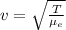
Where,

T = Tension

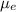`\mu_e`= Linear mass density

`v = \sqrt{(430)/(0.023)}`

`v = 136.7m/s`

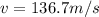
With this value the fundamental frequency would be

`f = (v)/(2L)`

`f = (136.7)/(2*1.3)`

`f = 52.6Hz`

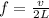
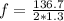
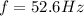
Finally the maximum speed is given with the relation between the Amplitude (A) and the Angular frequency, then

`V_(max) = A\omega`

`V_(max) = A(2\pi f)`

`V_(max) = (2.1*10^(-3))(2\pi 52.6)`

`V_(max) = 0.69m/s`

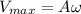
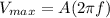
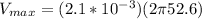
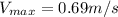
Therefore the correct answer is B.