Question

The machine is designed to cut lumber to 8 feet, but the actual cut length has some variation. Assume the true length X is uniformly distributed from 7.97 to 8.03. The PDF is represented at the right. You may assume: The mean of X is 8.00 The standard deviation of X is √0.005.

1. Find the mean and standard deviation of 4x

2. Find the mean and standard deviation of X1 + X2 + X3 + X4 where the terms are independent and with the same distribution above.

3. What is the better representation of the total length of four independently selected pieces of lumber laid end to end?

a) 4X b) X1 + X2 + X3 + X4 c) both are equally good d) none of the these.

4. Suppose you randomly selected 100 pieces of lumber (independent lengths) and compute the average length Xbar. What is the best way to describe the distribution of Xbar?

a) normal b) uniform c) gamma d) hypergeometric e) exponential

5. Suppose 100 pieces of lumber are laid end to end, and their lengths are independent. What is the probability that the TOTAL length, X1 + X2 + X3 + ⋯ + X100 = 100Xbar is within 3 inches (0.25 feet) of expected value?

Answer 1

1.) 0.2828

2.) 0.1414

3.) Option b

4.) Option a

5.) 0.2763

Explanation:

1.)

E(4X) = 4 * E(X) = 4 * 8 = 32

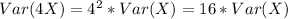
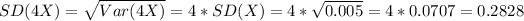
`Var(4X)=4^(2) *Var(X)=16*Var(X)`

`SD(4X)=√(Var(4X)) =4*SD(X)=4*√(0.005) =4*0.0707=0.2828`

2.)

`E(X_(1)+X_(2)+X_(3)+X_(4))=E(X_(1))+E(X_(2))+E(X_(3))+E(X_(4))=8+8+8+8=32`

`Var(X_(1)+X_(2)+X_(3)+X_(4))=Var(X_(1))+Var(X_(2))+Var(X_(3))+Var(X_(4))=0.0005+0.0005+0.0005+0.0005=0.02`

`SD(X_(1)+X_(2)+X_(3)+X_(4))=√(0.02) =0.1414`

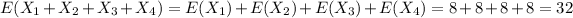
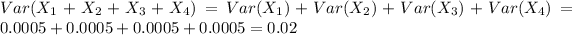
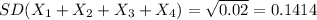
3.)

SD(4X) = 0.2828 > 0.1414

SInce SD(4X) >
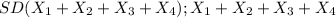`SD(X_(1)+X_(2)+X_(3)+X_(4));X_(1)+X_(2)+X_(3)+X_(4)` is more precise representation of total kenght. Hence it is better representation.

So the answer is the option b).

4.)

Since n=100 > 30, Xbar will be normal.

So the answer is the option a) Normal.

5.)

Since nµ is the expected value of sample total, i.e., nXbar, the required probability

= P(|nXbar - nµ|≤ 0.25), where n = 100 and µ = 8.00

= P[( ≤ {0.25/(σ√n)}]

= P[|Z| ≤ {0.25/(√0.005)√100}]

= P(|Z| ≤ 0.3535)

= P(-0.3535 < Z < 0.3535)

= P(Z < 0.3535) - P(Z < - 0.3535)

= 0.6381 – 0.3618 (from Z-distribution table)

= 0.2763

Hope this helps!