Answer:
12, 10, 6 (descending order)
Explanation:
 has real and rational roots if
has real and rational roots if
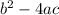 is a nonnegative perfect square.
is a nonnegative perfect square.
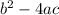 is called the discriminant.
is called the discriminant.
Let's calculate the discriminant of
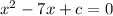 .
.
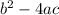

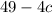
We want
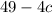 to be be positive or a zero perfect square.
to be be positive or a zero perfect square.
So let's first solve the inequality:
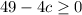
Add
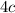 on both sides:
on both sides:
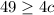
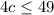
Divide both sides be 4:
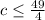
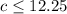 .
.
We know
 has to be a positive integer.
has to be a positive integer.
So we only need to evaluate
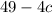 for 12 numbers.
for 12 numbers.
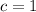 returns
returns
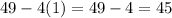 which is not a perfect square.
which is not a perfect square.
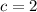 returns
returns
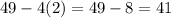 which is not a perfect square.
which is not a perfect square.
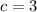 returns
returns
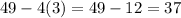 which is not a perfect square.
which is not a perfect square.
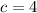 returns
returns
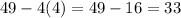 which is not a perfect square.
which is not a perfect square.
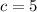 returns
returns
 which is not a perfect square.
which is not a perfect square.
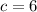 returns
returns
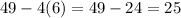 which is a perfect square.
which is a perfect square.
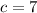 returns
returns
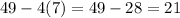 which is not a perfect square.
which is not a perfect square.
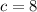 returns
returns
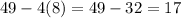 which is not a perfect square.
which is not a perfect square.
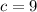 returns
returns
 which is not a perfect square.
which is not a perfect square.
 returns
returns
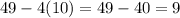 which is a perfect square.
which is a perfect square.
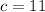 returns
returns
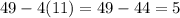 which is not a perfect square.
which is not a perfect square.
 returns
returns
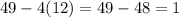 which is a perfect square.
which is a perfect square.