Question

If an object with a density 0.25 g/mL has a mass of 10 grams, and is added to a graduated cylinder filled with 50 mL of water, how high will the water in the graduated cylinder rise?

a) 50.25 mL b) 52.5 mL c) 60 mL d) 90 mL e) 150 mL

Answer 1

Answer : The correct option is, (d) 90 mL

Explanation :

First we have to calculate the volume of an object.

As we know that,

`Density=(Mass)/(Volume)`

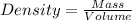
Given:

Density of an object = 0.25 g/mL

Mass of an object = 10 g

Now put all the given values in the above formula, we get:

`0.25g/mL=(10g)/(Volume)`

`Volume=40mL`

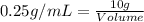
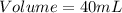
Thus, the volume of an object is 40 mL.

Now we have to calculate the height of the water in the graduated cylinder rise.

As we are given that:

The volume of water in graduated cylinder = 50 mL

The volume of an object = 40 mL

The height of the water in the graduated cylinder rise = Volume of water in graduated cylinder + Volume of an object

The height of the water in the graduated cylinder rise = 50 mL + 40 mL

The height of the water in the graduated cylinder rise = 90 mL

Therefore, the height of the water in the graduated cylinder rise will be, 90 mL