Answer:
61
Explanation:
Let's find the points
 and
and
 .
.
We know that the
 -coordinates of both are
-coordinates of both are
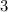 .
.
So let's first solve:
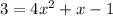
Subtract 3 on both sides:
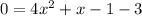
Simplify:
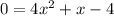
I'm going to use the quadratic formula,
 , to solve.
, to solve.
We must first compare to the quadratic equation,
 .
.
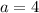
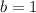
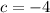
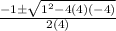
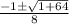

Since the distance between the points
 and
and
 is horizontal. We know this because they share the same
is horizontal. We know this because they share the same
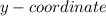 .This means we just need to find the positive difference between the
.This means we just need to find the positive difference between the
 -values we found for the points of
-values we found for the points of
 and
and
 .
.
So that is, the distance between
 and
and
 is:
is:
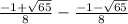
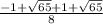
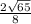
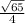
If we compare this to
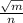 , we should see that:
, we should see that:
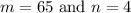 .
.
So
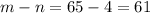 .
.