Question

Suppose that you just purchased a used car worth $12,000 in today’s dollars. Assume also that, to finance the purchase, you borrowed $10,000 from a local bank at 9% compounded monthly over two years. Assume that the average general inflation will run at 0.5% per month over the next two years.

a) What is the monthly payment charged by the bank? (5)

b) Determine the annual inflation-free interest rate for the bank, (5)

c) What equal monthly payments in terms of constant dollars over the next two years, are equivalent to the series of actual payments to be made over the life of the loan

Answer 1

A) Monthly Payment = $457

B) Inflation-free interest rate (month) = 0.2488%, (yearly) = 2.99%

C) Equal monthly payments = $429.75

Step-by-step explanation:

Requirement A

We know,

Present value of Annuity = PMT ×
`(1 - (1 + (i)/(m))^(-n × m) )/((i)/(m) )`

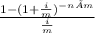
Given,

Present value = $10,000

Number of period, n = 2

Interest, i = 0.09

Monthly compounded, m = 12

Therefore,

$10,000 = PMT ×
`(1 - (1 + (0.09)/(12))^(-2*12) )/((0.09)/(12) )`

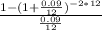
or, $10,000 = PMT × 21.8891

or, PMT = $457 (rounded to nearest whole number)

Therefore, monthly payment charged by the bank is $457.

Requirement B

We know, Inflation-free interest rate =
`(Monthly interest rate - Inflation rate)/(1 + Inflation rate)`

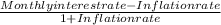
Given,

Monthly interest rate = i/m = 0.09/12 = 0.0075

Monthly inflation rate = 0.5% = 0.005

Therefore,

Inflation-free interest rate =
`(0.0075 - 0.005)/(1 + 0.005)`

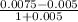
Inflation-free interest rate = 0.0024876 or, 0.2488% per month.

Therefore, the annual inflation-free interest rate for the bank = 0.2488% × 12 = 2.99%

Requirement C

We know, equal monthly payments = Borrowed Money × (Actual payment, monthly inflation-free interest rate, number of period)

Given,

Borrowed money = $10,000

Down Payment = $2,000

monthly inflation-free interest rate = 0.2488%

number of period = 24

Equal monthly payments = $10,000 × (Actual Payment, 0.2488%, 24)

But we have to use Present value of annuity formula to find the appropriate monthly payments

$10,000 = PMT ×
`(1 - (1 + 0.002488)^(-24) )/(0.002488)`

or, 10,000 = PMT × 23.2694

or, $429.75