Question

it takes mike 1 hour to get to work each day. he first rides the train, which travels at an average rate of 65 miles per hour. then he rides the subway train which travels at an average rate of 25 miles per hour. if the total distance that he travels from home to work is 61 miles how many minutes does mike spend riding the subway each morning?

Answer 1

6 minutes

Explanation:

We can turn the sentences into equations. As both the subway and the train have a given constant speed, then we don't need to worry about changing their values (due to things like slow down, accelerations, etc....). We will let x be the number of hours that Mike spends riding the train, and we will let y be the number of hours that Mike spends riding the subway, thus we can set up these two equations:

`65x+25y=61\\ x+y=1`

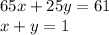
The first equation represents the total distance Mike must travel to get from home to work.

The second equation represents the total time Mike takes riding the subway and train.

Since we have a system of equations, we can solve it using multiple methods, distinctively:

Graphing

Substitution

Elimination

We will only do it in graphing and substitution as elimination will take too much time.

Method 1: Graphing

This is the easiest method, find any graphing calculator and insert these two equations and you will get this:

(see picture)

The point where both lines intersect will be our answer for x and y, which is:

`(0.9, 0.1)`

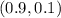
Since y is the number of hours that Mike is riding the subway, we can conclude that Mike rides the subway for one-tenth of an hour, which is 6 minutes.

Method 2: substitution

This is also a viable method when you don't have access to a graphing calculator. First, by the name of substitution, we want to find the value of one variable only in terms of the other variable, meaning that if we want to find the value of x, we will want to find it in values of y only, and vice versa. We can do this handily with the second equation, let's isolate x:

`x+y=1\\ x=1-y`

Afterward, we can substitute x into the first equation to find y as replacing x into the first equation will leave a single variable:

`x=1-y\\ 65x+25y=61\\ 65(1-y)+25y=61\\ 65-65y+25y=61\\ 65-40y=61\\ -40y=-4\\ y=(1)/(10)`

If we needed to find x, we will replace y in the second equation, but in this case, we just needed to find y, so there's no need to find x. We know that y is the number of hours that Mike is riding the subway, and we also found that y is one-tenth, thus, Mike spends 6 minutes (which is one-tenth of an hour) riding the subway.

Wow this question is posted 2 years ago