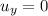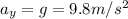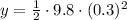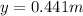Question

a rifle is aimed directly at the bulls eye of a target 75 meters away. if the bullet has a speed of 250 m/s, how far below the bulls eye will the bullet hit

Answer 1

Step-by-step explanation:

Given

Distance of target d=75 m

velocity of bullet v=250 m/s

First taking horizontal motion

as there is no acceleration is horizontal direction therefore
`a_x=0`

`d=ut+(1)/(2)a_xt^2`

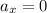
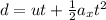
where u=initial velocity

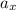`a_x`=acceleration

t=time

`75=250* t`

`t=0.3 s`

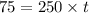
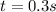
In this time Vertical distance moved by Bullet is

`y=u_yt+(1)/(2)a_yt^2`

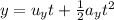
here
`u_y=0`

`a_y=g=9.8 m/s^2`

`y=(1)/(2)\cdot 9.8\cdot (0.3)^2`

`y=0.441 m`