Question

Given congruent triangles name the corresponding sides and corresponding angles

Triangle ABC is congruent to Triangle ADC
(Image is provided)

Answer 1

See explanation

Explanation:

Given
`\triangle ABC\cong \triangle ADC`

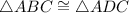
According to the order of the vertices,

• side AB in triangle ABC (the first and the second vertices) is congruent to side AD in triangle ADC (the first and the second vertices);

• side BC in triangle ABC (the second and the third vertices) is congruent to side DC in triangle ADC (the second and the third vertices);

• side AC in triangle ABC (the first and the third vertices) is congruent to side AC in triangle ADC (the first and the third vertices);

• angle BAC in triangle ABC is congruent to angle DAC in triangle ADC (the first vertex in each triangle is in the middle when naming the angles);

• angle ABC in triangle ABC is congruent to angle ADC in triangle ADC (the second vertex in each triangle is in the middle when naming the angles);

• angle BCA in triangle ABC is congruent to angle DCA in triangle ADC (the third vertex in each triangle is in the middle when naming the angles);