Answer :
(a) The number of radon atoms will remain after 12 days is,
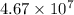
(b) The number of radon nuclei have decayed by this time will be,

Explanation :
For part (a) :
Half-life = 3.82 days
First we have to calculate the rate constant, we use the formula :
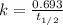
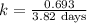

Now we have to calculate the number of radon atoms will remain after 12 days.
Expression for rate law for first order kinetics is given by:
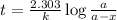
where,
k = rate constant =
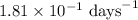
t = time passed by the sample = 12 days
a = initially number of radon atoms =

a - x = number of radon atoms left = ?
Now put all the given values in above equation, we get

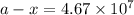
Thus, the number of radon atoms will remain after 12 days is,
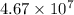
For part (b) :
Now we have to calculate the number of radon nuclei will have decayed by this time.
The number of radon nuclei have decayed = Initial number of radon atoms - Number of radon atoms left
The number of radon nuclei have decayed =
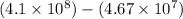
The number of radon nuclei have decayed =

Thus, the number of radon nuclei have decayed by this time will be,
