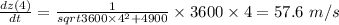Question

A railroad track and a road cross at right angles. An observer stands on the road and watches an eastbound train traveling at 60 meters per second. At how 70 meters south of the crossing. How many meters per second is the train moving away from the observer 4 seconds after it passes through the intersection?

Answer 1

After 4 s of passing through the intersection, the train travels with 57.6 m/s

Solution:

As per the question:

Suppose the distance to the south of the crossing watching the east bound train be x = 70 m

Also, the east bound travels as a function of time and can be given as:

y(t) = 60t

Now,

To calculate the speed, z(t) of the train as it passes through the intersection:

Since, the road cross at right angles, thus by Pythagoras theorem:

`z(t) = \sqrt{x^(2) + y(t)^(2)}`

`z(t) = \sqrt{70^(2) + 60t^(2)}`

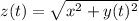
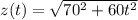
Now, differentiate the above eqn w.r.t 't':

`(dz(t))/(dt) = (1)/(2).\frac{1}{sqrt{3600t^(2) + 4900}}* 2t* 3600`

`(dz(t))/(dt) = \frac{1}{sqrt{3600t^(2) + 4900}}* 3600t`

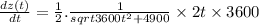
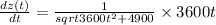
For t = 4 s:

`(dz(4))/(dt) = \frac{1}{sqrt{3600* 4^(2) + 4900}}* 3600* 4 = 57.6\ m/s`