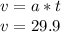Question

A 45.2-kg wagon is towed up a hill inclined at 18.5∘ with respect to the horizontal. The tow rope is parallel to the incline and has a tension of 191 N in it. Assume that the wagon starts from rest at the bottom of the hill, and neglect friction. How fast is the wagon going after moving 83.8 m up the hill?

Answer 1

The speed is 29.9 m/s

Step-by-step explanation:

The force created from gravity due to the wagon mass is:

`F=m*g*sin(18.5)\\F=45.2*9.8*sin(18.5)\\F=140.55`

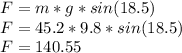
140.55 N pull the wagon down. Two parallel rope with tension of 191N creates 382 N on the wagon. Therefore:

`T_(total)=382-140.55=241.45`

241.45 N force is pulling up the wagon. Then we need to find the acceleration of the wagon under this force:

`F=m*a\\241.45=45.2*a\\a=5.34`

acceleration is 5.34 m/s^2. The distance is multiplication of acceleration and square of the time.

`x=1/2*a*t^2\\83.8=0.5*5.34*t^2\\t=5.6`

After 5.6 second the wagon will ride 83.8 m up to hill. And the speed of wagon at that point is:

`v=a*t\\v=29.9`