Question

Which of the following is equal to the expression below?

Answer 1

C)

Explanation:

Answer 2

Explanation:

This can be simplified into

`8^{(1)/(3)}*320^{(1)/(3)}`

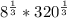
which is saying that you are taking the cubed root of each of those bases. The cubed root of 8 comes out evenly, to 2 (since 2*2*2 = 8). The cubed root of 320 is not so simple. To find it, find the complete factorization of 320. 320 factors to: 5 * 2*2*2*2*2*2 or

`\sqrt[3]{320}= \sqrt[3]{5*2^6}`

Split that 2^6 up into increments of 3's to make the simplifying a bit easier:

`\sqrt[3]{5*2^3*2^3}`

Because the index (the little number sitting in the bend of the radial sign) matches the power on both the 2's we can pull both the 2's out front, leaving:

`4\sqrt[3]{5}`

but don't forget that we already found that the cubed root of 8 was 2, so multiply that 2 by the 4 to get:

`8\sqrt[3]{5}`