Answer:
The maximum amount of profit the company can make is of $1577.
Explanation:
The profit is given by the following equation:

Which is a quadratic equation.
Maximum value of a quadratic function:
Suppose we have a quadratic function in the following format:

The maximum value of the function is given by:
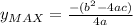
In this question, we have that:
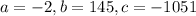 . So
. So
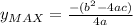

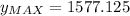
To the nearest dollar, $1577
The maximum amount of profit the company can make is of $1577.