Question

In this exercise we look at memory locality properties of matrix computation. The following code is written in C, where elements within the same row are stored contiguously. Assume each word is a 32-bit integer.

(P&H 5.1, §5.1) for (I=0; I<8; I++) for (J=0; J<8000; J++) A[I][J]=B[I][0]+A[J][I];

a.How many 32-bit integers can be stored in a 16-byte cache block?

b.References to which variables exhibit temporal locality?

c.References to which variables exhibit spatial locality?

Answer 1

a)
`32 bits * (1 byte)/(8 bits)= 4 bytes`

`16 bits *(1 integer)/(4 bytes)= 4 integers`

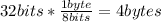
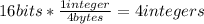
b) Locally variables represent the counters for the cicle on this case the variables I and J are from 0 to 8000. So these two variables (I and J) represent the variable that exhibit temporcal locality

c) We are storing elements in a Row Major format A[I][J] so then are the variables that represent spatialy locality. The matrix A on this case will have at least 8000 columns because
`0 \leq J \leq 8000` so we will have minimum 8000 elements between A[J][I] and A[J+1][I].

Step-by-step explanation:

Assuming this code:

for (I=0; I<8; I++)

for(J=0;J<8000;J++)

A[I][J]=B[I][0] +A[J][I]

We assume that this code is write on C language.

In this exercise we look at memory locality properties of matrix computation. The following code is written in C, where elements within the same row are stored contiguously. Assume each word is a 32-bit integer.

Part a

First we need to remember that 1 byte= 8 bits. And we can convert 32 bits to bytes like this:

`32 bits * (1 byte)/(8 bits)= 4 bytes`

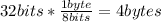
And since the cycle containes 16 bytes we can find the number of integers like this:

`16 bits *(1 integer)/(4 bytes)= 4 integers`

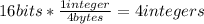
Part b

Locally variables represent the counters for the cicle on this case the variables I and J are from 0 to 8000. So these two variables (I and J) represent the variable that exhibit temporcal locality

Part c

We are storing elements in a Row Major format A[I][J] so then are the variables that represent spatialy locality. The matrix A on this case will have at least 8000 columns because
`0 \leq J \leq 8000` so we will have minimum 8000 elements between A[J][I] and A[J+1][I].