Answer:
Option B.
Explanation:
Given information:
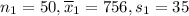
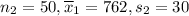
We need to find 95% confidence interval estimate for the difference between the means of two normally distributed populations.
Formula for confidence interval:

From the standard normal table it is clear that the z value at 95% confidence interval is 1.96.
Substitute the given values in the above formula.
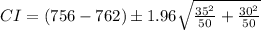
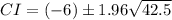
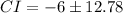
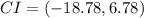
The lower confidence limit is −18.78.
Therefore, the correct option B.