Answer:
Explanation:
This is an exponential equation that is solved by taking the natural log of both sides. The equation is
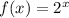
If we are looking for x when f(x) = 64, then
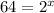
Take the natural log of both sides:
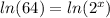
The rules of logs allows us to bring the x down in front:

Divide both sides by ln(2) to get:
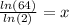
Do this on your calculator to get that x = 6.
You could also have just gone right to your calculator and started raising 2 to consecutive powers starting at like 3 or 4 to eventually get that 2 to the 6th power is equal to 64, but for the basics of solving log equations, you need to know how to do this.