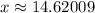Answer:
The exact answer in terms of radicals is
![x = 5*\sqrt[3]{25}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pztdx9sz1vzhx6hv93clsodlc2c8tl747u.png)
The approximate answer is
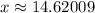 (accurate to 5 decimal places)
(accurate to 5 decimal places)
===============================================
Work Shown:
Let
![y = \sqrt[5]{x^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zpk45is8s8rpw90tkumu5vwvpf8zx6i8z6.png)
So the equation reduces to -7 = 8-3y
Let's solve for y
-7 = 8-3y
8-3y = -7
-3y = -7-8 ... subtract 8 from both sides
-3y = -15
y = -15/(-3) ... divide both sides by -3
y = 5
-----------
Since
![y = \sqrt[5]{x^3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zpk45is8s8rpw90tkumu5vwvpf8zx6i8z6.png) and y = 5, this means we can equate the two expressions and solve for x
and y = 5, this means we can equate the two expressions and solve for x
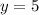
![\sqrt[5]{x^3} = 5](https://img.qammunity.org/2020/formulas/mathematics/middle-school/t3bmdl4bkn3jjnw33q0di1ux0c929jutg6.png)
 Raise both sides to the 5th power
Raise both sides to the 5th power

![x = \sqrt[3]{3125}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/6tsf57u1ovtkq0jmphhorsyuo2xj0xssn6.png) Apply cube root to both sides
Apply cube root to both sides
![x = \sqrt[3]{125*25}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4k0gv9o8xz9i51r6ebueawtcgnvif10hs7.png)
![x = \sqrt[3]{125}*\sqrt[3]{25}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/m49qnf5qlgaiqdraap1ntslrp9dajozmoi.png)
![x = \sqrt[3]{5^3}*\sqrt[3]{25}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lfqnqn2mhzrbfwlbqt9ixirlv4rqmndx5e.png)
![x = 5*\sqrt[3]{25}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pztdx9sz1vzhx6hv93clsodlc2c8tl747u.png)