Answer:
The negative 4 translates the original function 4 units horizontally to the right
Explanation:
The transformed graph is
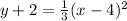
and the parent function is
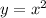
We need to find what effect does the "4" in the transformed function have with respect to the parent function. Lets look at a general form of a transformed quadratic function and see what each variable means:
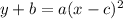
This is the general form.
- +b means the graph is vertically translated b units down
- -b would have meant the graph would have been vertically translated b units up
- a transforms the parent by vertically stretching or compressing
- -c means the parent is shifted c units right
- +c would have meant the parent will be shifted c units left
In our transformed graph, we have a "-4", this means, according to the rules above, that:
the parent function is shifted 4 units to the right