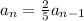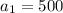Answer:
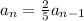
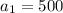
----------------------or one might prefer the answer so that
 is a decimal:
is a decimal:

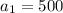
Explanation:
The recursive form got a geometric sequence is
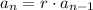 with a term given such as the first term,
with a term given such as the first term,
 .
.
 can be determined by choosing a term from the sequence and dividing by it's previous term.
can be determined by choosing a term from the sequence and dividing by it's previous term.
That is
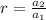 or
or
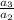 or so on...
or so on...
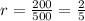
So the recursive form for this sequence is: