Answer:
The distance traveled can be found by kinematics equations

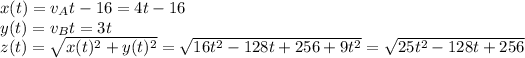
Step-by-step explanation:
The initial position of Car B is denoted as origin. Car A started at -16 km, and moving right. Car B started at origin and moving up. z is the magnitude of the vector with components x and y.
The relation can be found by pythagorean theorem.
For checking the solution, we can find the positions at t = 4h. Car A is at the origin, and Car B is 12 km north of origin. z = 12.