Question

HELPP!!!!!!!!!!!!!!!!

Answer 1

Explanation:

We'll take this step by step. The equation is

`8-3\sqrt[5]{x^3}=-7`

Looks like a hard mess to solve but it's actually quite simple, just do one thing at a time. First thing is to subtract 8 from both sides:

`-3\sqrt[5]{x^3}=-15`

The goal is to isolate the term with the x in it, so that means that the -3 has to go. Divide it away on both sides:

`\sqrt[5]{x^3}=5`

Let's rewrite that radical into exponential form:

`x^{(3)/(5)}=5`

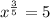
If we are going to solve for x, we need to multiply both sides by the reciprocal of the power:

`(x^{(3)/(5)})^{(5)/(3)}=5^{(5)/(3)}`

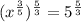
On the left, multiplying the rational exponent by its reciprocal gets rid of the power completely. On the right, let's rewrite that back in radical form to solve it easier:

`x=\sqrt[3]{5^5}`

Let's group that radicad into groups of 3's now to make the simplifying easier:

`x=\sqrt[3]{5^3*5^2}` because the cubed root of 5 cubed is just 5, so we can pull it out, leaving us with:

`x=5\sqrt[3]{5^2}` which is the same as:

`x=5\sqrt[3]{25}`