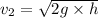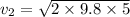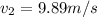Question

Assume that the side of the water tank is punctured 5.0 m below the top of the water, and that atmospheric pressure is 1.0 × 10⁵ N/m². What is the approximate speed of the water flowing from the hole?

Answer 1

Answer:9.89 m/s

Step-by-step explanation:

Given

Punctured hole is h=5 m below the top surface

Atmospheric Pressure
`P_(atm)=10^5 N/m^2`

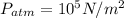
Applying Bernoulli's theorem

Assuming Point 1 at top and 2 at Punctured hole

`P_1+\rho gy_1+(1)/(2)\rho v_1^2=P_2+\rho gy_2+(1)/(2)\rho v_2^2`

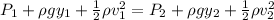
Since Pressure at top and bottom is same therefore
`P_1=P_2`

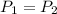
velocity at top can be taken as zero as water is not flowing

`(1)/(2)\rho v_2^2=\rho g(y_1-y_2)`

`v_2=√(2g* h)`

`v_2=√(2* 9.8* 5)`

`v_2=√(98)`

`v_2=9.89 m/s`