Question

(1 pt) If y=e5t is a solution to the differential equationd2ydt2−11dydt+ky=0,find the value of the constant k and the general solution to this equation.k= y= (Use constants A, B, etc., for any constants in your solution formula.)

Answer 1

`y = A e^(5t) + B e^(6t)`

Explanation:

given,

`y = e^(5t)`

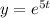
and equation

y" - 11 y' + k y = 0...............(1)

now,

`y' = 5 e^(5t)`

`y`

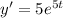
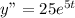
Putting value in equation (1)

`25 e^(5t) - 11(5 e^(5t)) + k e^(5t) = 0`

`- 30 + k = 0`

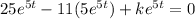
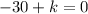
k = 30

now, differential equation becomes

y" - 11 y' +30 y = 0

( D² - 11 D + 30) y = 0

writing Auxiliary equation'

m² - 11 m + 30 = 0

(m - 5)(m-6) = 0

m = 5,6

now,

`y = A e^(5t) + B e^(6t)`