Question

The Correlation Coefficient for a relationship is - 0.95. What percentage of the dependent variable in the correlation is due purely to chance? (Answer with a percent rounded to the hundredths decimal place. Include the % sign.)

Answer 1

The unexplained variance would be 100-90.25 % = 9.75. And that correspond to the percentage of the dependent variable in the correlation is due purely to chance

Explanation:

Previous concepts

Pearson correlation coefficient(r), "measures a linear dependence between two variables (x and y). Its a parametric correlation test because it depends to the distribution of the data. And other assumption is that the variables x and y needs to follow a normal distribution".

In order to calculate the correlation coefficient we can use this formula:

`r=(n(\sum xy)-(\sum x)(\sum y))/(√([n\sum x^2 -(\sum x)^2][n\sum y^2 -(\sum y)^2]))`

On this case we got that r =-0.95

In order to find the % of variance explained by the model we need to calculate the determination coefficient given by:

`R^2 = (-0.95)^2 = 0.9025`

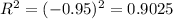
And that means this : "90.25% of the variation of y is explained by the variation in x"

So then the unexplained variance would be 100-90.25 % = 9.75. And that correspond to the percentage of the dependent variable in the correlation is due purely to chance