Answer:
a)
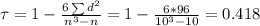
b)
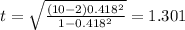
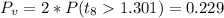
So using the significance level provided we see that
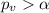 so we have enough evidence to FAIL to reject the null hypothesis that the Spearman Correlation coeffcint is equal to 0.
so we have enough evidence to FAIL to reject the null hypothesis that the Spearman Correlation coeffcint is equal to 0.
Explanation:
Dataset given
Number IQ Job performance
1 100 16
2 115 38
3 108 23
4 98 20
5 120 48
6 147 56
7 132 47
8 85 57
9 105 28
10 110 35
Previous concepts
Spearman's Rank correlation coefficient "is a value that measure the strength and direction (negative or positive) of a relationship between two variables. The result will always be between 1 and minus 1".
Solution to the problem
Part a
In order to calculate the sparman correlation coefficient we need to order the dataset like this:
Number IQ(x) Rank1 Job performance (y) Rank2 d d^2
1 85 10 57 1 9 81
2 98 9 20 9 0 0
3 100 8 16 10 -2 4
4 105 7 28 7 0 0
5 108 6 23 8 -2 4
6 110 5 35 6 -1 1
7 115 4 38 5 -1 1
8 120 3 48 3 0 0
9 132 2 47 4 -2 4
10 147 1 56 2 -1 1
The difference d is dfined as

Then
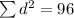
And now we can calculate the sparman correlation coeffcient like this:
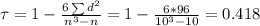
Part b
The system of hypothesis on this case are:
H0:

H1:
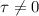
The statistic to check the hypothesis is given by:
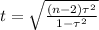
And replacing the value obtained we got:
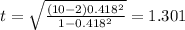
The degrees of freedom on this case are given by:
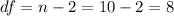
And the p value since is a bilateral test is given by:
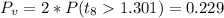
So using the significance level provided we see that
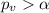 so we have enough evidence to FAIL to reject the null hypothesis that the Spearman Correlation coeffcint is equal to 0.
so we have enough evidence to FAIL to reject the null hypothesis that the Spearman Correlation coeffcint is equal to 0.