We can compute the integral directly: we have
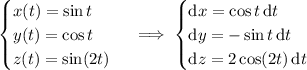
Then the integral is

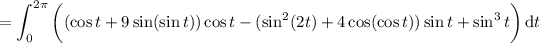
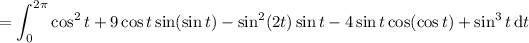
You could also take advantage of Stokes' theorem, which says the line integral of a vector field
 along a closed curve
along a closed curve
 is equal to the surface integral of the curl of
is equal to the surface integral of the curl of
 over any surface
over any surface
 that has
that has
 as its boundary.
as its boundary.
In this case, the underlying field is
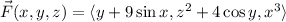
which has curl
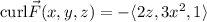
We can parameterize
 by
by
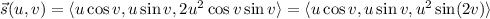
with
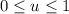 and
and
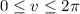 .
.
Note that when viewed from above,
 has negative orientation (a particle traveling on this path moves in a clockwise direction). Take the normal vector to
has negative orientation (a particle traveling on this path moves in a clockwise direction). Take the normal vector to
 to be pointing downward, given by
to be pointing downward, given by

Then the integral is
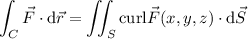
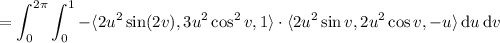
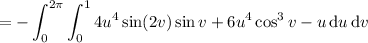
Both integrals are kind of tedious to compute, but personally I prefer the latter method. Either way, you end up with a value of
 .
.