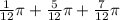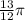Answer:
Explanation:
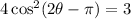
We want to first isolate the trig expression.
We will do this by first dividing both sides by 4 and then taking the square root of both sides.

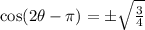
Let's clean up the right hand side a little:

Break time to think about something to help us solve the above:
So
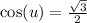 when
when
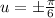 in the one cycle of
in the one cycle of
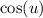 .
.
So
 when
when
 in the one cycle of
in the one cycle of
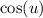 .
.
Back to it:

Solving one of those equations:
 when
when
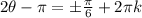
Let's solve for
 .
.
Add
 on both sides:
on both sides:
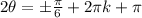
Divide both sides by 2:
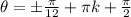
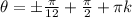
Now we also have to solve the other:
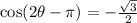 when
when
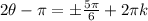
Let's solve for
 .
.
Add
 on both sides:
on both sides:

Divide both sides by 2:
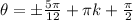
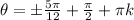
So the full set of solutions is:
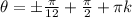
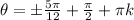
---------------------------------------------------------------------------------
I'm going to evaluate these expressions for some integer
 :
:
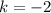 we have:
we have:
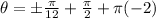
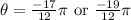
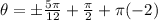
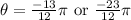
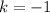 we have:
we have:
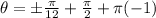
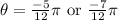
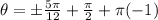
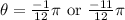
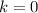 we have:
we have:
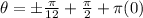


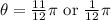
 we have:
we have:
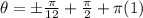

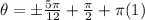
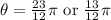
Anyways the values will keep getting larger from here.
We can see that the smallest positive values happen when
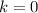 .
.
So we have the first smallest is: \frac{1}{12}\pi[/tex].
The second smallest is
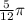 .
.
The third smallest is
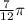 .
.
So the sum of these numbers are: