Answer:
See proof below
Explanation:
One way to solve this problem is to "add a zero" to complete the required squares in the expression of xy.
Let
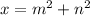 and
and
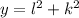 with
with
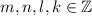 . Multiplying the two equations with the distributive law and reordering the result with the commutative law, we get
. Multiplying the two equations with the distributive law and reordering the result with the commutative law, we get
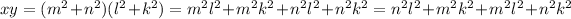
Now, note that
 by the commutativity of rational integers. Add this convenient zero the the previous equation to obtain
by the commutativity of rational integers. Add this convenient zero the the previous equation to obtain
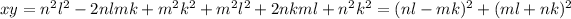 , thus xy is the sum of the squares of
, thus xy is the sum of the squares of
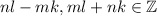 .
.