Answer:
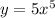
Explanation:
Functions of the form:
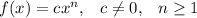
There are two cases with these kind of funtions:
First case:
n is even:
If n is even and c>0 the function tends to ∞. On the other hand, if n is even and c<0 the function tends to -∞. The range in every case is:
![n=even,\hspace{6}c>0\\R=[0,\infty)\\\\n=even,\hspace{6}c<0\\R=(-\infty,0]](https://img.qammunity.org/2020/formulas/mathematics/high-school/g8u84kof8is5rk6pkvnm3xxjo93g2wddjc.png)
Second case:
n is odd:
If n is odd and c>0 the function tends to ∞ for every x>0 and tends to -∞ for every x<0. On the other hand If n is odd and c<0 the function tends to -∞ for every x>0 and tends to ∞ for every x<0. The range in every case is:
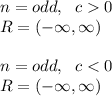
According to this the first two option doesn't fit with the graph because n=2=even. So it must be the last two options. As you can see the graph tends to ∞ for every x>0 and tends to -∞ for every x<0, hence c>0.
Therefore the answer is:
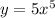
I attached you the graph in order that you can corroborated the answer.