Question

Suppose we replace the mass in the video with one that is four times heavier. How far from the free end must we place the pivot to keep the meter stick in balance?

50 cm (in the middle)
90 cm (10 cm from the weight)
75 cm (25 cm from the weight)
10 cm
25 cm

Answer 1

We must place the pivot to keep the meter stick in balance at 90 cm (10 cm from the weight) from the free end.

Answer: Option B

Step-by-step explanation:

In initial stage, the meter stick’s mass and mass hanged in meter stick at one end are same. Refer figure 1, the mater stick’s weight acts at the stick’s mid-point.

If in case, the meter stick is to be at balanced form, then the acting torques sum would be zero. So,

`m * g *(x)+((m * g)(x-50 \mathrm{cm}))=0`

`(m * g * x)-(50 * m * g)+(m * g * x)=0`

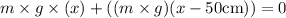
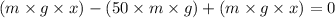
Taking out ‘mg’ as common and we get

`2 x-50=0`

`2 x=50`

`x=(50)/(2)=25 \mathrm{cm}`

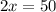
Hence, the stick should be pivoted at a distance of,

`x^(\prime)=100 \mathrm{cm}-25 \mathrm{cm}=75 \mathrm{cm}`

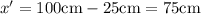
So, the stick should be pivoted at a distance of 75 cm at the free end

Now, replace mass with another mass. i.e., four times the initial mass (as given)

If in case, the meter stick is to be at balanced form, then the acting torques sum would be zero. So,

`4 m g(x)+(m g)(x-50 c m)=0`

`4 m g x+m g x-50 m g=0`

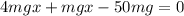
Taking out ‘mg’ as common and we get

`5 x=50`

`x=(50)/(5)=10 \mathrm{cm}`

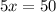
Hence, the stick should be pivoted at a distance of,

`x^(\prime)=100 \mathrm{cm}-10 \mathrm{cm}=10 \mathrm{cm}`

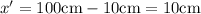
So, the stick should be pivoted at a distance of 10 cm from the free end.

Therefore, the option B is correct 90 cm (10 cm from the weight).