Question

The binding energy of a potassium chloride molecule (K0) is 4.43 eV. The ionization energy of a potassium atom is 4.3 eV,and the electron affinity of chlorine is 3.6 eV. Use these data to estimate the equilibrium separation between the two atomsin the KCI molecule. Explain why your result is only an estimate and not a precise value.

Answer 1

To solve this problem we will apply the concept given by the internal energy of the molecular union, for which this is equal to bending energy and ionization energy minus all that energy product of the electron affinity. Our values are given as:

• Boding energy of KCl is 4.43 eV
• Ionization energy of K is 4.3eV
• Electron affinity of Cl is 3.6eV

The potential energy of K and Cl atoms is

U = Bending energy +(ionization energy - electron affinity)

`U = 4.43eV+ (4.3-3.6)eV`

`U = 5.03eV`

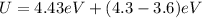
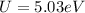
Through Coulomb's law to define electrostatic energy we have to

`U = (1)/(4\pi \epsilon_0)\cdot (q_1q_2)/(r_0)`

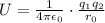
Where,

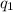`q_1` is the charge on one body,

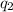`q_2` is the charge on the other body,

r is the distance between them,

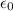`\epsilon_0` is the electric constant or permittivity of free space or permittivity of the vacuum

Re-arrange to find the distance,

`r_0 = (1)/(4\pi \epsilon_0)\cdot (q_1q_2)/(U)`

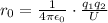
Replacing,

`r_0 = 9*10^9*(((1.6*10^(-19))^2)/((5.03)(1.6*10^(-19))))`

`r_0 = 2.8*10^(-10)m`

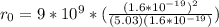
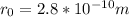
Since the two atoms are not an ideal point loader, it is necessary to take the given data as an estimate.