Question

Rewrite the following expression.

x9/7

Answer 1

`\displaystyle x\sqrt[7]{x}^2`

Explanation:

According to the Definition of Rational Exponents [part II], we can rewrite this exponential expression as a radical:

`\displaystyle \sqrt[n]{a}^m = a^{(m)/(n)} \\ \\ x\sqrt[7]{x}^2 = x^{(9)/(7)} \\ \\ \\ [\sqrt[7]{x}^2][\sqrt[7]{x}^7] = x\sqrt[7]{x}^2`

I am joyous to assist you anytime.

Answer 2

Hence the simplified expression is y =
`x * \sqrt[7]{x^(2)}`

Explanation:

The given expression is y =
`x^{(9)/(7) }`

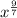
We have to rewrite this without fractions in the power of x.

For that we have to use the laws of exponents to simplify the expression. This can be easily done as shown below.

y =
`x^{(9)/(7) }`

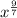
y =
`\sqrt[7]{x^(9)}`

=
`\sqrt[7]{x^(7)* x^(2)}`

We can simplify this as

`\sqrt[7]{x^(7)}* \sqrt[7]{x^(2)}` =
`x * \sqrt[7]{x^(2)}`

Hence the simplified expression is y =
`x * \sqrt[7]{x^(2)}`