Answer:
Question 30
Null hypothesis:
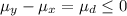
Alternative hypothesis:
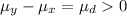
So the best option is:
a. μd<=0 and μd > 0
Question 31
So the p value is higher than any significance level given, so then we can conclude that we FAIL to reject the null hypothesis that the difference mean between after and before is lower or equal than 0.
Then the best option is:
b. He cannot reject the null hypothesis
Question 32
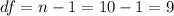
b. 9
Question 33
Since we FAIL to reject the null hypothesis we don't have enough evidence to conclude that we don't have significant differences at 1% of significance.
Step-by-step explanation:
Previos concepts
A paired t-test is used to compare two population means where you have two samples in which observations in one sample can be paired with observations in the other sample. For example if we have Before-and-after observations (This problem) we can use it.
Question 30
The system of hypothesis for this case are:
Null hypothesis:
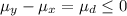
Alternative hypothesis:
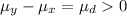
So the best option is:
a. μd<=0 and μd > 0
Question 31
We have the statistic already calculate t=0.709
The next step is calculate the degrees of freedom given by:
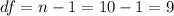
Now we can calculate the p value, since we have a right tailed test the p value is given by:
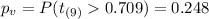
And we can calculate it using the following excel code:
"=1-T.DIST(0.709,9,TRUE)"
So the p value is higher than any significance level given, so then we can conclude that we FAIL to reject the null hypothesis that the difference mean between after and before is lower or equal than 0.
Then the best option is:
b. He cannot reject the null hypothesis
Question 32
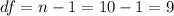
b. 9
Question 33
b. No
Since we FAIL to reject the null hypothesis we don't have enough evidence to conclude that we don't have significant differences at 1% of significance.