Question

The shorter leg of the right triangle is 7 inches shorter than the longer leg. The hypotenuse of 7 inches longer than the shorter leg. Find the side lengths of the triangle.

Answer 1

The shorter leg is 21 inches

The longer leg is 28 inches

The hypotenuse is 35 inches

Explanation:

The correct question is

The shorter leg of the right triangle is 7 inches shorter than the longer leg. The hypotenuse is 7 inches longer than the longer leg. Find the side lengths of the triangle

Let

x ----> the shorter leg of the right triangle

y ----> the longer leg of the right triangle

z ----> the hypotenuse of the right triangle

we know that

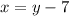`x=y-7` ---> equation A

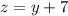`z=y+7` ----> equation B

Applying the Pythagorean Theorem

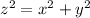`z^2=x^2+y^2` ---> equation C

substitute equations A and B in equation C

`(y+7)^2=(y-7)^2+y^2`

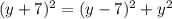
solve for y

`y^2+14y+49=y^2-14y+49+y^2`

`y^2-28y=0`

`y(y-28)=0`

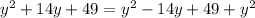
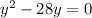
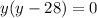
The solution for y=28 in

Find the value of x

`x=28-7=21\ in`

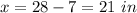
Find the value of z

`z=28+7=35\ in`

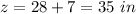
therefore

The shorter leg is 21 inches

The longer leg is 28 inches

The hypotenuse is 35 inches

Answer 2

The data has been redefined to make the question have a feasible solution. You can adjust it to better fit to your own problem.

Answer:

Shorter leg: 21 inches

Longer leg: 28 inches

Hypotenuse: 35 inches

Explanation:

Right Triangles

Their distinctive attribute is they have a right angle (90°) and a longer side called the hypotenuse. The relationship between the shorter legs and the hypotenuse is given by the Pythagoras's theorem. Being x and y the legs of a right triangle and z its hypotenuse, then

`z^2=x^2+y^2`

The question explains that the shortest leg is 7 inches shorter than the other leg. If we set x as the length of the longer leg, then the shortest leg will be (x-7) inches long. The next statement has a mistake. It says the hypotenuse is 7 inches longer than the shorter leg. It's impossible since it would make the hypotenuse the same length of the longer leg. To make this question solvable, let's assume the hypotenuse is 7 inches longer than the longer leg, so it will be (x+7) inches long. Let's set up the Pythagora's formula

`(x+7)^2=x^2+(x-7)^2`

Expanding the squares

`x^2+14x+49=x^2+x^2-14x+49`

Rearranging

`x^2+x^2-14x+49-x^2-14x-49=0`

Simplifying

`x^2-28x=0`

Factoring

`x(x-28)=0`

The solutions are x=0 or x=28

Since the side of a trangle cannot be zero or negative, we'll only keep the feasible solution :

`x=28\ inches`

The shorter leg is

`x-7=21\ inches`

And the hypotenuse

`x+7=35\ inches`