Question

prove that if the number of terms of an A.P is odd then the middle term is the A P between the first and last term???​

Answer 1

Prove that if the number of terms of an A.P is odd then the middle term is the A.M between the first and last term???​

Answer:

Proved that when number of terms of an A.P is odd then the middle term is the A .M between the first and last term

Solution:

To prove: If the number of terms of an A.P is odd then the middle term is the A .M between the first and last term

Proof:

Let the arithmetic progression be:

a, a + d, a + 2d, ........., (2n + 1) terms

As the number of terms are odd, the nth term is (2n + 1)

The middle term of (2n + 1)th term is:

`\rightarrow ((2n + 1 + 1))/(2) = (2n + 2)/(2)= (n + 1)`

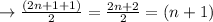
Hence middle term is (n + 1)th term

The formula for nth term of arithmetic progression is:

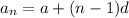`a_n = a + (n - 1)d` ------- (i)

Where n is the terms location and "d" is the common difference between terms

Thus middle term is: (n + 1)th term

From (i)

`\text{ middle term } = a + (n + 1 - 1)d = a + nd` ----- (ii)

Arithmetic mean between first and last term:

The nth term is (2n + 1)

Hence nth term (last term) is:

From (i)

`\rightarrow a + (2n + 1 - 1)d = a + 2nd`

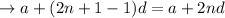
So Arithmetic mean between 1st & last term is:

First term of A.P = a

Arithmetic mean between first and last term = (first term + last term)/2

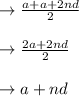`\rightarrow (a + a + 2nd)/(2)\\\\\rightarrow (2a + 2nd)/(2)\\\\\rightarrow a + nd` ----- (iii)

Thus from steps (ii) and (iii)

Middle term = AM of 1st and last terms [Proved]

Thus proved that when number of terms of an A.P is odd then the middle term is the A .M between the first and last term