Question

At the same instant that a 0.50 kg ball is dropped from 25 m above Earth, a second ball, with a mass of .25 kg, is thrown straight upward from Earth's surface with an initial speed of 15 m/s.

They move along nearby lines and pass each other without colliding. At the end of the 2s:

A. what is the height above Earth's surface of the center of mass of the two-ball system?

B: what is the velocity of the center of mass of the two-ball system?

C: what is the magnitude of the acceleration of the center of the mass of the two-ball system?

Answer 1

A. 7.1m

B. 3.55m/s

C. 1.775m/s^2

Step-by-step explanation:

First step is to identify given parameters;

Ball 1: m₁ = 0.5kg, u (initial velocity) =0, t = 2seconds

Ball 2: m₂ = 0.25kg, u = 15m/s, t = 2seconds

Second step: we determine the y-coordinate of ball 1 after 2 seconds, using the equation of motion under gravity as shown below;

`y = ut - (gt^2)/(2)`

`y_(1) = 0 X 2 - (9.8 X2^2)/(2)`

`y_(1) = -19.6m`

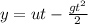
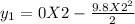
Recall, that the ball was thrown from a height of 25m, total y-coordinate of ball 1 after 2 seconds becomes 25m +(-19.6m)

[tex]y_{1} = 5.4m[/tex]

Third step: we determine the y-coordinate of ball 2 after 2 seconds

`y_(2) = 15 X 2 - (9.8 X2^2)/(2)`

`y_(2) = 10.4m`

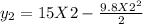
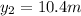
Fourth step: we determine the y-component of the center mass of the two balls

`y = (m_(1)y_(1) +m_(2)y_(2))/(m_(1) +m_(2) )`

`y = ((0.5)X(5.4) +(0.25) X (10.4))/((0.5 +0.25) )`

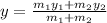
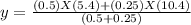
y = 7.1m

Fifth step: we solve B part of the question; velocity of the center mass of the two balls

`Velocity = (distance of center mass of the two balls (y))/(time)`

`velocity = (7.1 m)/(2 s)`

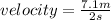
velocity = 3.55m/s

Sixth step: we solve C part of the question; acceleration of the center mass of the two balls

`acceleration = (velocity)/(time)`

`acceleration = (3.55)/(2)`

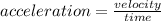
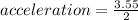
acceleration = 1.775 m/s^2