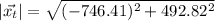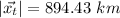Question

A plane takes off from an airport and flies at a speed of 400km/h on a course of 120° for 2 hours. the plane then changes its course to 210° and continues in this direction for 1 hour. How far is the plane from the airport at the end of this time?

Answer 1

Distance from the airport = 894.43 km

Explanation:

Displacement and Velocity

The velocity of an object assumed as constant in time can be computed as

`\displaystyle \vec{v}=\frac{\vec{x}}{t}`

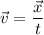
Where
`\vec x` is the displacement. Both the velocity and displacement are vectors. The displacement can be computed from the above relation as

`\displaystyle \vec{x}=\vec{v}.t`

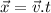
The plane goes at 400 Km/h on a course of 120° for 2 hours. We can compute the components of the velocity as

`\displaystyle \vec{v_1}=<400\ cos\ 120^o,400\ sin\ 120^o>`

`\displaystyle \vec{v_1}=<-200,\ 200√(3)>\ km/h`

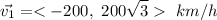
The displacement of the plane in 2 hours is

`\displaystyle \vec{x_1}=\vec{v_1}.t_1=<-200,200√(3)>.(2)`

`\displaystyle \vec{x_1}=<-400,400√(3)>km`

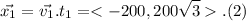
Now the plane keeps the same speed but now its course is 210° for 1 hour. The components of the velocity are

`\displaystyle \vec{v_2}=<400\ cos210^o,400\ sin 210^o>`

`\displaystyle \vec{v_2}=<-200√(3),-200>km/h`

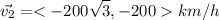
The displacement in 1 hour is

`\displaystyle \vec{x_2}=\vec{v_2}.t_2=<-200√(3),-200>.(1)`

`\displaystyle \vec{x_2}=<-200√(3),-200>km`

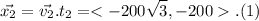
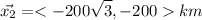
The total displacement is the vector sum of both

`\displaystyle \vec{x_t}=\vec{x_1}+\vec{x_2}=<-400,400√(3)>+<-200√(3),-200>`

`\displaystyle \vec{x_t}=<-400-200√(3),400√(3)-200>km`

`\displaystyle \vec{x_t}=<-746.41\ km,492.82\ km>`

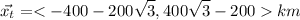
The distance from the airport is the module of the displacement:

`\displaystyle |\vec{x_t}|=√((-746.41)^2+492.82^2)`

`\displaystyle |\vec{x_t}|=894.43\ km`