Question

A wave with a frequency of 60 Hz is traveling along a string whose linear mass density is 230 g/m and whose tension is 65 N. If the wave is to transfer energy at a rate of 75 W, what should the amplitude of the wave be?

Answer 1

To develop this problem we will use the concepts related to Speed in a string that is governed by Tension (T) and linear density (µ)

`V = \sqrt{(T)/(\mu)}`

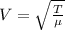
Our values are given as:

`f = 60Hz\\\mu = 230 g/m = 0.230kg/m\\T = 65N\\P = 75w`

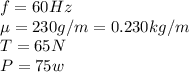
Replacing we have that the velocity is

`V = \sqrt{(T)/(\mu)}`

`V = \sqrt{(65)/(0.230)}`

`V = 16.81m/s`

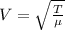
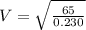
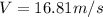
From the theory of wave propagation the average power wave is given as

`P =(1)/(2) \mu \omega^2 A^2 V`

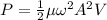
Where,

A = Amplitude

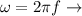`\omega = 2\pi f \rightarrow` Angular velocity

`A^2 = (2P)/(\mu \omega^2 V)`

`A^2 = (2P)/(\mu (2\pi f)^2 V)`

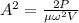
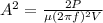
Replacing,

`A^2 = \sqrt{(2(75))/((0.230)(2\pi 60)^2(16.81))}`

`A = 0.0165m`

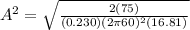
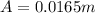
Therefore the amplitude of the wave should be 0.0165m