Question

bucket contains 3 red balls and 2 blue balls. Two balls are drawn simultaneously and at random. what is the probability that one ball is blue, given taht at least one ball is red

Answer 1

The probability of drawing one blue ball given that at least one ball is red is 1/3.

Step-by-step explanation:

To find the probability that one ball is blue given that at least one ball is red, we first need to determine the sample space. Since there are 5 balls in total (3 red and 2 blue), there are a total of 10 possible outcomes when drawing 2 balls simultaneously without replacement.

To calculate the probability, we need to consider the different combinations of balls that satisfy the given condition. There are 3 combinations: RD, DR, and RR (where R represents a red ball and D represents a blue ball). Out of these combinations, only the combination RD satisfies the condition of having one blue ball and at least one red ball.

Therefore, the probability of drawing one blue ball given that at least one ball is red is 1/3.

Answer 2

Answer: The required probability is 0.86.

Step-by-step explanation: Given that a bucket contains 3 red balls and 2 blue balls, out of which two balls are drawn simultaneously at random.

We are to find the probability that one ball is blue, given that at least one ball is red.

Let A denotes the event that at least one of two balls is red and B denotes the event that one ball is blue.

So,

`n(A)=^3C_1*^2C_1+^2C_2=3*2+1=7.`

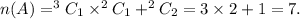
And, B∩A = event that one ball is red and one ball is blue.

So,

`n(B\cap A)=^3C_1* ^2C_1=3*2=6.`

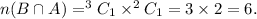
Then, we have

`P(A)=(n(A))/(^5C_2)=(7)/(10),\\\\\\P(B\cap A)=(n(B\cap A))/(^5C_2)=(6)/(10).`

Therefore, the conditional probability of B, given A is

`P(B/A)=(P(B\cap A))/(P(A))=((6)/(10))/((7)/(10))=(6)/(7)=0.86.`

Thus, the required probability is 0.86.