Answer:
The number of bright-dark fringe is 42
Solution:
As per the question:
Wavelength of light,
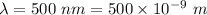
Length of the glass cell, x = 3.73 cm = 0.0373 m
Refractive index,
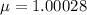
Now,
To calculate the bright-dark fringe shifts, we use the formula given below:

Now, substituting the appropriate values in the above formula:
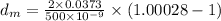
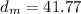 ≈ 42
≈ 42