Question

A study of 10 different weight loss programs involved 500 subjects. Each of the 10 programs had 50 subjects in it. The subjects were followed for 12 months. Weight change for each subject was recorded. The researcher wants to test the claim that all ten programs are equally effective in weight loss. (a) Which statistical approach should be used? (i) confidence interval (ii) t-test (iii) ANOVA (iv) Chi square (b) Explain the rationale for your selection in (a). Specifically, why would this be the appropriate statistical approach?

Answer 1

a) (iii) ANOVA

b) The ANOVA test is more powerful than the t test when we want to compare group of means.

Explanation:

Previous concepts

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

If we assume that we have
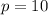`p=10` groups and on each group from
`j=1,\dots,p=10` we have
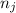`n_j` individuals on each group we can define the following formulas of variation:

`SS_(total)=\sum_(j=1)^p \sum_(i=1)^(n_j) (x_(ij)-\bar x)^2`

`SS_(between)=SS_(model)=\sum_(j=1)^p n_j (\bar x_(j)-\bar x)^2`

`SS_(within)=SS_(error)=\sum_(j=1)^p \sum_(i=1)^(n_j) (x_(ij)-\bar x_j)^2`

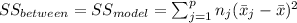
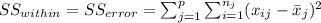
And we have this property

`SST=SS_(between)+SS_(within)`

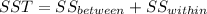
Solution to the problem

Part a

(i) confidence interval

False since the confidence interval work just when we have just on parameter of interest, but for this case we have more than 1.

(ii) t-test

Can be a possibility but is not the best method since every time that we conduct a t-test we have a chance that we commit a Type I error.

(iii) ANOVA

This one is the best method when we want to compare more than 1 group of means.

(iv) Chi square

False for this case we don't want to analyze independence or goodness of fit, so this one is not the correct test.

Part b

The ANOVA test is more powerful than the t test when we want to compare group of means.