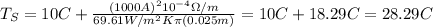Question

A 25 mm diameter high voltage power line has an electrical resistance of 10-4 Ohm/m, and is transmitting current of 1000 A.

If ambient air at temperature Tinfinity =10 degreeC and wind freestream velocity is uinfinity = 10 m/s is in cross-flow over the power line (assume it to be a long copper cylinder), what is its surface temperature?

[Assume a temperature of 300K while looking for properties of copper and air in heat transfer property tables]

Answer 1

`T_S =10 C + ((1000A)^2 10^(-4) \Omega/m)/(69.61 W/m^2 K \pi(0.025m))=10C +18.29 C=28.29 C`

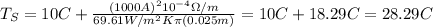
Step-by-step explanation:

For this case we need to make some assumptions. For example the properties not change in the time. steady conditions and that we just have conduction on the cylinder creating radial conduction.

The next step would be calculate the properties for each element at 300K using th table A.4

Air

`P= 1 atm , T_f \approx 300K`
`v=15.89x10^(-6) m^2/s , k=0.0262 W/mK, Pr= 0.707`

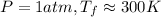
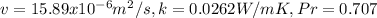
Copper

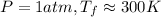`P= 1 atm , T_f \approx 300K` , k=400 W/mK[/tex]

Solution to problem

Now in order to solve the problem we can use conservation of energy assuming a control volume of unit length, and we have the following equation:

`E_g = I^2 R_e = q. =\bar h \pi D(T_s -T_a)`

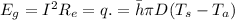
And we have this :

`Re_D =(VD)/(v)=(10m/s (0.025m))/(15.89x10^(-6) m^2/s)=15733.17`

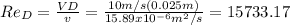
From the correlation of Churchill we can find
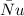`\bar Nu` like this:

`\bar Nu_(D) =0.3 +(0.62 Re^(1/2)_D Pr^(1/3))/([1+(0.4/Pr)^(2/3)]^(1/4))[1+((Re_D)/(282000))^(5/8)]^(4/5)`

And if we replace we got:

`\bar Nu_(D) =0.3 +(0.62 15733.17^(1/2)_D 0.707^(1/3))/([1+(0.4/0.707)^(2/3)]^(1/4))[1+((15733.17)/(282000))^(5/8)]^(4/5) =66.17`

Then we can find the value for
`\bar h`

`\bar h = Nu_D (k)/(D)=66.17 (0.0263 W/mK)/(0.025m)=69.61 W/m^2 K`

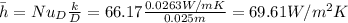
And finally we can calculate the surface temperature with this formula:

`T_S =T_a + (I^2 R_e)/(\bar h \pi D)`

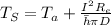
And replacing we have:

`T_S =10 C + ((1000A)^2 10^(-4) \Omega/m)/(69.61 W/m^2 K \pi(0.025m))=10C +18.29 C=28.29 C`