Question

Find the area of the shaded segment of the circle.

(Round to the nearest tenth as needed.)

Answer 1

Area of the shaded region = 87.5 cm²

Explanation:

Area of the shaded region = Area of the sector - Area of the triangle

Area of the sector =
`(\theta)/(360)* (2\pi r)`

Here, θ = Central angle subtended by the arc

r = radius of the circle

Area of the given sector =
`(120)/(360)* (\pi r^(2))`

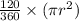
= 48π

= 150.796 cm²

From ΔABC,

Central angle BAC = 120°

Since, AD is an angle bisector of ∠BAC,

m∠BAD = m∠CAD = 60°

∠ADC = 90° [By theorem, line from the center to any chord is a perpendicular bisector of the chord in a circle)

Now, cos(60) =
`(AD)/(AC)`

`(1)/(2)=(AD)/(12)`

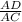
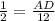
AD = 6

Similarly, sin(60) =
`(DC)/(AC)`

`(√(3) )/(2)=(DC)/(12)`

DC =
`6√(3)`

Since, BC = 2(DC) =
`12√(3)`

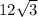
Area of ΔABC =
`(1)/(2)(\text{Height})(\text{Base})`

=
`(1)/(2)(AD)(BC)`

=
`(1)/(2)(6)(12√(3))`

=
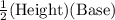
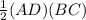
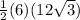
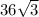`36√(3)` cm²

= 62.35 cm²

Now area of the shaded region = (150.796 - 62.35)

= 87.456

≈ 87.5 cm²