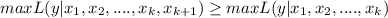Question

Give a sample proof that the likelihood of the data cannot decrease if we add a new link to the network and recompute the maximum likelihood parameter values

Answer 1

See the proof below

Explanation:

Let's assume that our random variable of interest is Y and we have a set of parameters
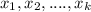`x_1,x_2,....,x_k` in the original network.

And let's assume that we add an additional parameter
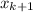`x_(k+1)` and we want to see if the likehood for
`x_1, x_2,.....,x_k, x_(k+1)`

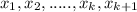
We don't know the distribution for each parameter
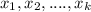`x_1,x_2,....,x_k` but we can say that the likehood function for the original set of parameters is given by:

`F=L(y| x_1,x_2,....,x_k)`

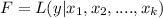
And in order to maximize this function we need to take partial derivates respect to each parameter like this:

`(dF)/(dx_i) =(dL)/(dx_i), i=1,2,....,k`

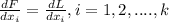
We just need to set up the last derivate equal to zero and solve for the parameters who satisfy the condition.

If we add a new parameter the new likehood function would be given by:

`F=L(y| x_1,x_2,....,x_k,x_(k+1))`

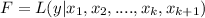
And in order to maximize this function again we need to take partial derivates respect to each parameter like this:

`(dF)/(dx_i) =(dL)/(dx_i), i=1,2,....,k,k+1`

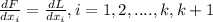
We are ssuming that we have the same parameters from 1 to k for the new likehood function. So then the likehood for the data would be unchanged and if we have more info for the likehood function we are maximizing the function since we are adding new parameters in order to estimate the function.

`max L(y| x_1,x_2,....,x_k,x_(k+1)) \geq max L(y| x_1,x_2,....,x_k)`