Question

A solid sphere, soild cylinder, and a hollow pipe all have equal masses and radii and are of uniform density.

If the three are released simultaneously at the top of an inclinded plane and roll without slipping, which one will the bottom first?

A) Solid cylinder

B) Solid sphere

C) hollow pipe

Answer 1

We will use the conservation of energy. For all the objects the following is true:

`(1)/(2)I\omega^2 + (1)/(2)mv^2 = mgh`

The moment of inertia for the objects are

`I_(sphere) = (2)/(5)mr^2\\I_(cylinder) = (1)/(2)mr^2\\I_(pipe) = mr^2`

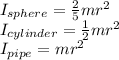
So, the energy equations for the sphere are

`(1)/(2)(2)/(5)mr^2((v)/(r))^2 + (1)/(2)mv^2 = mgh\\(7)/(10)mv^2 = mgh\\v_(sphere) = \sqrt{(10gh)/(7)}`

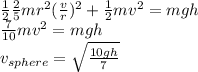
The energy equations for the cylinder are

`(1)/(2)(1)/(2)mr^2((v)/(r))^2 + (1)/(2)mv^2 = mgh\\(3)/(4)mv^2 = mgh\\v_(cylinder) = \sqrt{(4gh)/(3)}`

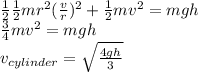
The energy equations for the pipe are

`(1)/(2)mr^2((v)/(r))^2 + (1)/(2)mv^2 = mgh\\mv^2 = mgh\\v_(pipe) = √(gh)`

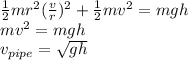
The sphere has the highest velocity at the bottom. Therefore, it arrives the bottom first. Then the cylinder, and the pipe arrives the last.

Step-by-step explanation:

Since all the objects has the same mass and initial potential energy, their final kinetic energy at the bottom is the same as well. Therefore, the object with the lowest moment of inertia will have the highest velocity. By definition, the moment of inertia is the resistance to rotation. So, the object with the lowest resistance will have the highest velocity.